CodeIQ 「スロット・マシン」 問題
Kawazoe (@riverplus) n 個のリール(数字が描かれている部分です)を持つスロットマシンを回します。 各リールには、0 から 9 のいずれかの数字がランダムに出ます。 このとき、「最も多く出現した数字の出現回数」に等しいドルが賞⾦として得られます。
例えば n = 6 のスロットマシンを考えましょう。 各リールに、左から順に 7 7 5 1 0 7 という数字が出たとします。 このとき、7 の数字が最も多く 3 回出現していますので、賞⾦は 3 ドルです。
リールの数字が 0 2 0 9 2 6 のとき、賞⾦は 2 ドルです。 リールの数字が 1 2 3 4 5 6 のとき、賞⾦は 1 ドルです。 リールの数字が 8 8 8 8 8 8 のとき、賞⾦は 6 ドルです。
このスロットマシンを 1 回まわしたときの賞⾦の期待値を F(n) とします。 例えば F(1) = 1,F(2) = 1.1,F(3) = 1.29 となることが確かめられます。
■ 第1問 (Normal) F(6) の値を求めて下さい(四捨五⼊は不要です)。
■ 第2問 (Hard) F(12) の値を求めて下さい(四捨五⼊は不要です)。
import numpy as np from scipy import misc def bunkatu(n,x): if n<=0: return [[]] if x==1: return [[1]*n] s1=[] if n>=x: s1=bunkatu(n-x,x) for i in range(len(s1)): s1[i].insert(0,x) s2=(bunkatu(n,x-1)) s1.extend(s2) return(s1) def haiti(bunkatu): n=sum(bunkatu) bn=[] bunkatu.append(-1) cnt=0 for i in range(len(bunkatu)-1): cnt+=1 if bunkatu[i]!=bunkatu[i+1] or bunkatu[i+1]==(-1): bn.append(cnt) cnt=0 bunkatu.pop() hoge=1 for b in bunkatu: hoge=hoge*misc.comb(n,b) n=n-b for b in bn: hoge=hoge/misc.factorial(b) return(hoge) ''' 最大k個揃う確率をP(k)とすると P(k)=g(n,k)/10^n g(n,k):最大でk個揃うパターンの総数 n:スロットの数 g(n,k)はたとえば n=8,k=3とすると[3,3,2],[3,2,2,1]等,8を最大3になるような自然数で分割し、 各々の分割に対して (それらを配置するパターンの数A)×(数の割り振りパターンB) Aは例えば[3,3,2]だったら 8C3*5C3*2÷2!通り (3組、3組がダブルカウントだから2!で割る) Bはたとえば3種類だったら10*9*8通り A*Bを足し上げます。 nを最大x個の和で表す分割パターンの列挙は、bunkatu(n,x)で行います。 xを使う場合と使わない場合に分けて、再帰でリストを返しています。 ''' #期待値の計算 n=12 s=0 for k in range(1,n+1): hoge=bunkatu(n-k,k) for i in range(len(hoge)): hoge[i].insert(0,k) tmp=0 for h in hoge: m=len(h) hh=np.arange(10,10-m,-1) #数の振り分けパターン hh=np.product(hh) tmp+=haiti(h)*hh s+= k*tmp/(10**n) print(s)
Wine Quality
練習。
UCI Machine Learning Repository: Wine Quality Data Set
hoge=sample(1:1599,900) #900件をトレーニング用に train=wine[hoge,] test=wine[-hoge,] # 0.66くらい相関がある特徴があったけど、とりあえずただの線形回帰 train.lm=lm(data=train,quality~.) wine.pred=predict(train.lm,newdata = test) mse(test$quality,wine.pred) #√mseです #0.6576445 #ランダムフォレスト #mtryはTunerfより train.rf=randomForest::randomForest(data=train,quality~.,mtry=3) wine.pred.rf=predict(train.rf,newdata = test) mse(test$quality,wine.pred.rf) #0.6297493 #多少良くなった
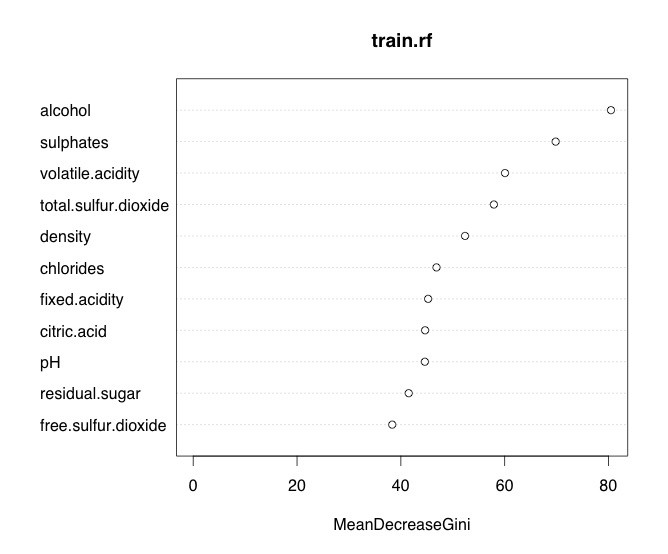
正則化、PCAでは特に削れる特徴量はなさそうでした。 quality=7,8の時の誤差が大きいのは気になるけど(-1.0くらい)、どーなんでしょう。
夏場は炭酸が多いけど、赤ワインは基本毎日飲んでます。800円付近のネロ・ダヴォラ、サンライズ、ボルドーあたり。就職したらデイリーワインに1500円くらい使ってみたいですね(´;ω;`)ブワッ
t→x,yの擬似相関
下の例で計算すると0.96。
線形トレンド
観測方程式
の状態空間で、x,y(変数名の方)の残差の相関をstanで計算すると-0.12程度になった。
N.t=60 mu.x = numeric(N.t) x = numeric(N.t) mu.y = numeric(N.t) x=y=c() mu.x[1] = mu.y[1] = 10 s1 = 2 s2 = 1 for (t in 1:(N.t - 1)) { x[t] = rnorm(1, mu.x[t], s1) mu.x[t + 1] = rnorm(1, mu.x[t] + 1, s2) y[t] = rnorm(1, mu.y[t], s1) mu.y[t + 1] = rnorm(1, mu.y[t] + 1, s2) } x[N.t] = rnorm(1, mu.x[N.t - 1], s1) y[N.t] = rnorm(1, mu.y[N.t - 1], s1) scodeaa=" data{ int N; real x[N]; real y[N]; } parameters{ real sigma_x; real sigma_y; real trend_x[N]; real trend_y[N]; real sigma_trend_x; real sigma_trend_y; } model{ for(t in 3:N){ trend_x[t]~normal(trend_x[t-1]*2-trend_x[t-2],sigma_trend_x); trend_y[t]~normal(trend_y[t-1]*2-trend_y[t-2],sigma_trend_y); } x~normal(trend_x,sigma_x); y~normal(trend_y,sigma_y); } " library(rstan) fit=stan(model_code = scodeaa,data = list(N=N.t,x=x,y=y),chain=1,iter=200) la=extract(fit) tr_x=apply(la$trend_x,2,mean) tr_y=apply(la$trend_y,2,mean) cor(x-tr_x,y-tr_y) #>[1] -0.1202267